Современные технологии включают множество наукоемких процессов, в которых вещества могут находиться в экстремальных или экзотических условиях. Высокие температуры и давления, взаимодействие со стенками наноканалов и нанопор представляют сложность для экспериментального измерения и точного теоретического предсказания свойств веществ.

Фото: dan cristian padure / unsplash.com
Фото: dan cristian padure / unsplash.com
Сложные взаимодействия жидкостей со стенками могут возникать при добыче нефти и газа. Породы, в которых находится жидкость, представляют собой пористую среду. Газ, чтобы попасть в скважину, должен, как говорят, «профильтроваться» через эти поры. В настоящее время идет переход к добыче из все более низкопроницаемых месторождений, в которых поры могут иметь нанометровые размеры. При течении через них нужно учитывать, что на свойства жидкости и газа начинает влиять взаимодействие со стенкой. Для точного предсказания характеристик течения нужно учесть не только общие свойства, такие как температуру, плотность, давление и вязкость, но также форму и деформируемость молекул в процессе движения.
Один из способов смоделировать свойства веществ на микроуровне — это метод молекулярной динамики. В этом методе мы рассматриваем каждую молекулу как отдельную взаимодействующую частицу и решаем уравнения движения. В целом это похоже на моделирование движения планет или взаимодействия объектов при столкновениях в компьютерных играх, только форма взаимодействия подбирается специальным образом, чтобы описывать желаемое вещество или смесь веществ.
Такие расчеты гораздо сложнее, чем расчет методом сплошной среды, поэтому смоделировать можно только небольшое количество вещества, от нескольких сот до нескольких миллионов молекул. Временной промежуток, на котором идет моделирование, тоже очень короткий — несколько миллиардных долей секунды. И даже для этого нужны ресурсы суперкомпьютера (хотя то, что можно было назвать «суперкомпьютером» десять лет назад, сейчас может быть домашним компьютером, хотя и из верхнего сегмента). Из-за таких ограничений масштабов обычно моделируется не весь физический процесс полностью, а только его ключевые части, в которых вещество попадает в какие-то экзотические или сложно исследуемые состояния. Например, такими методами моделируется вещество под воздействием мощных ударных волн, но обычно только в области, где температура и степень сжатия максимальны.
В нашей работе нам интересны коэффициенты вязкости при высоких давлениях, кривые фазового равновесия, течения жидкостей внутри наноразмерных пор. Подобрав модели молекулярного взаимодействия для нужных веществ, мы можем рассчитать эти величины. Этот вычислительный метод имеет преимущества по сравнению с вычислениями, основанными на теории сплошной среды, а также по сравнению с натурными экспериментами.

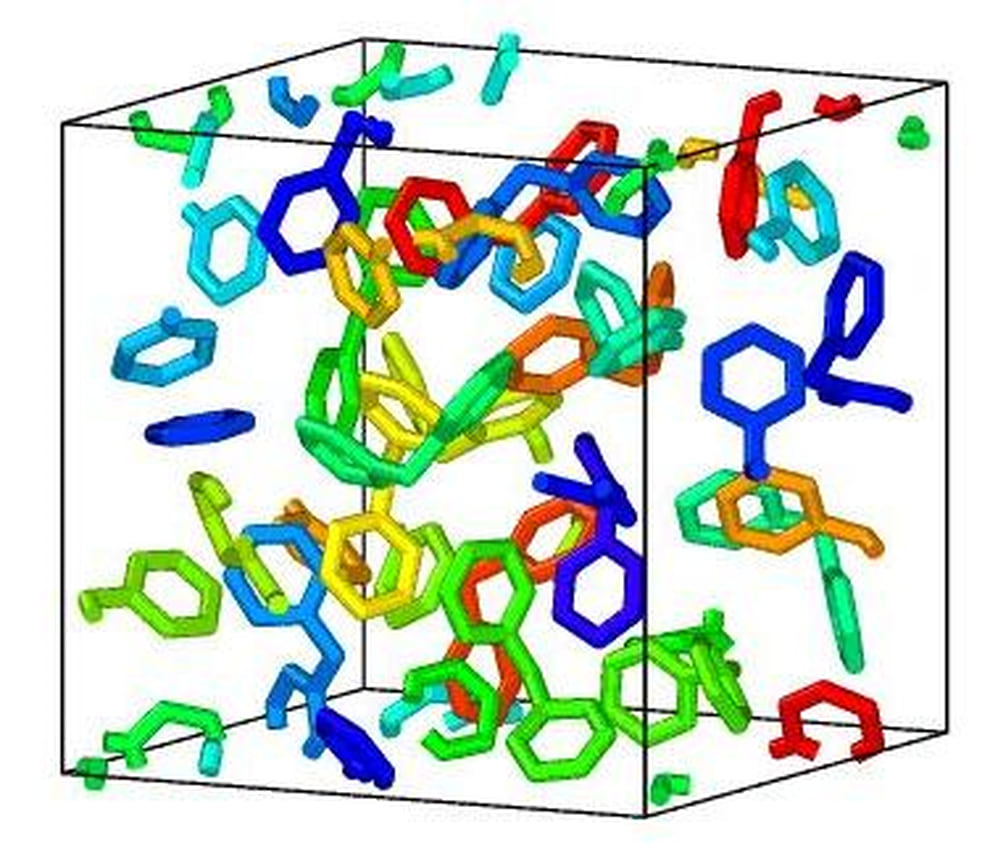
Схема молекулярно-динамического расчета фазового равновесия в смеси метан-бутан
Фото: Писарев В.В.
Схема молекулярно-динамического расчета фазового равновесия в смеси метан-бутан
Фото: Писарев В.В.
Для решения уравнений сплошной среды требуется вводить отдельно модель фазовых переходов, модель вязкости, модель термодинамических свойств и т. д. В методе молекулярной динамики наиболее важная часть — достаточно точная модель молекулярных взаимодействий. Если они воспроизводятся близко к реальности, все остальные свойства получаются из движения молекул «автоматически».
Для экспериментальных измерений разных свойств требуются разные установки, порой весьма сложные. В компьютерном моделировании весь спектр свойств получается из расчетов при помощи одного и того же компьютера.
Проведение расчетов может быть быстрее, чем подготовка и проведение эксперимента, а также не имеет проблем с чистотой веществ и работой с токсичными компонентами.
Применение молекулярно-динамического моделирования, таким образом, может существенно сократить количество необходимых экспериментальных данных для понимания ряда процессов, а также может использоваться как дополнение к экспериментам для лучшего понимания механизма физических процессов на наномасштабах.
Одна из наших работ, например, была посвящена исследованию устойчивости различных структур гидрата водорода — особой формы льда с растворенным в ней газом. Эксперименты показывали новую фазу гидрата при высоких давлениях, но не могли точно определить структуру. Молекулярное моделирование позволило сократить число возможных структур, согласующихся с экспериментальными данными, с четырех до двух. Более того, возможно, что экспериментально наблюдалась смесь этих двух структур.
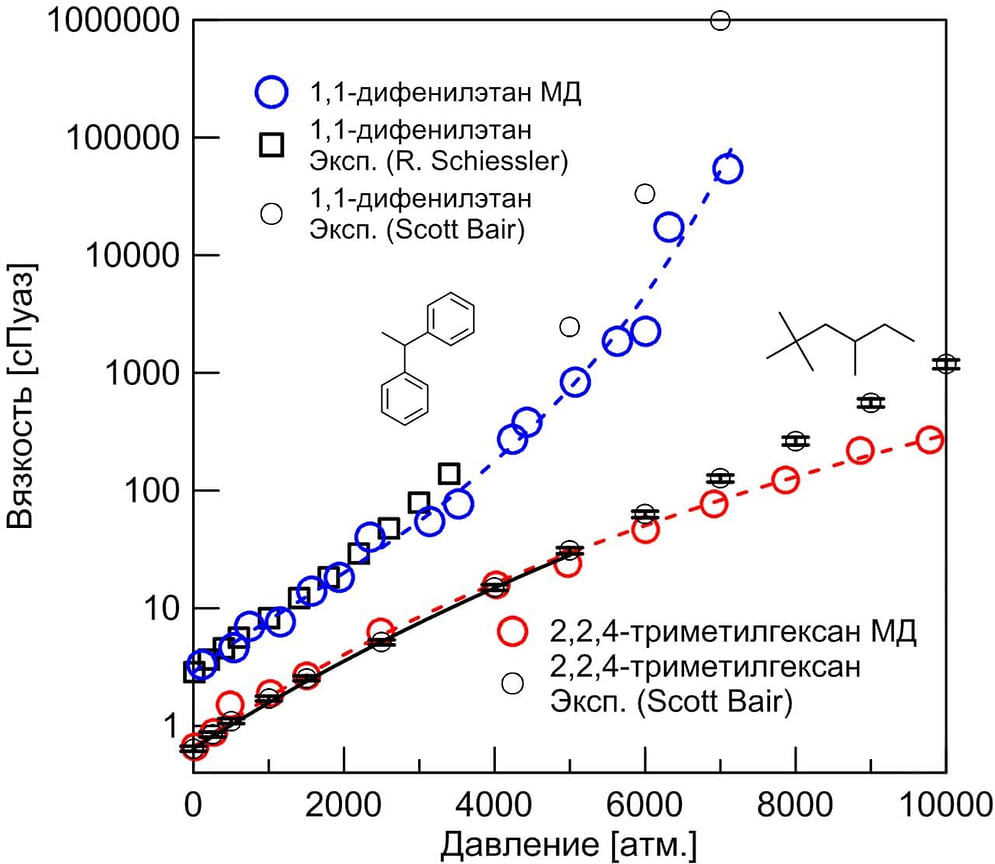
В другом цикле работ мы рассчитывали вязкость жидких углеводородных смесей, являющихся моделями природных нефтегазовых систем и смазочных материалов. Мы показали, что достаточно продвинутые молекулярные модели могут предсказывать вязкость жидкостей не только при нормальных условиях, но и при высокой степени сжатия, до 5–6 тыс. атмосфер. Также молекулярное моделирование уже давно применяется для сокращения экспериментального поиска при разработке лекарств, а в последнее время проникает в исследования для химической промышленности.
Поскольку в молекулярном моделировании как размеры, так и время рассматриваемых процессов ограниченны, для распространения результатов на привычные нам масштабы используется так называемый многомасштабный подход — данные молекулярного моделирования используются как вход для теории с менее подробным уровнем рассмотрения, но позволяющей с теми же вычислительными затратами описать систему большего размера. Мы сейчас работаем над вопросом определения параметра проницаемости среды на основе рассчитанных свойств жидкости в наноразмерных порах, эмпирических данных о распределении формы и размеров пор в пластовых породах и материале породы. Это позволит распространить данные молекулярного моделирования через методы сплошной среды на более крупные масштабы как по пространству, так и по времени.
Результаты исследований могут быть применены для гидродинамического моделирования и оптимизации режимов добычи углеводородов, а также при разработке топливных и смазочных смесей.