Рак нельзя вылечить, но можно победить. Решающую битву с ним ведут, и это поражает самих врачей, — математики
Прикладная математика

Слева направо: аспирант Иван Егоров, профессор Александр Братусь, аспирант Йордан Тодоров рассчитывают стратегии выживания для раковых больных
Фото: Иван Ерофеев
24 декабря аспирант факультета вычислительной математики и кибернетики МГУ Иван Егоров представляет к защите диссертацию "Обобщение метода характеристик Коши для численно-аналитических методов решения задач синтеза оптимального управления". В одной из четырех частей этой работы решается задача поиска стратегии лечения рака, при которой число больных и здоровых клеток находится в пределах, гарантирующих жизнедеятельность пациента в течение максимально возможного времени. Вместе с немецким аспирантом из Болгарии Йорданом Тодоровым он доказал существование стратегии лечения (и продемонстрировал его модель), при которой чередуются периоды интенсивной терапии и релаксации, и при этом в течение всего времени количество больных клеток не превышает заданного предела, а число здоровых клеток и иммунных клеток не уменьшается ниже заданного значения. Кроме того, поскольку само лекарственное средство токсично, то его концентрация в организме ограничена сверху. Молодые ученые аналитическим путем нашли поверхность переключений (то есть точек, в которых должна происходить смена интенсивной терапии на релаксацию) в расширенном фазовом пространстве управляемой динамической системы, описывающей процесс лечения, с учетом заданных ограничений.
Стратегия выживания
Медики уже почти смирились с тем, что окончательно уничтожить раковые клетки в организме невозможно: за миллионы лет эволюции (еще древние египтяне пытались лечить рак мышьяком) те научились противостоять любому "оружию", придуманному человеком. При этом химиотерапевтическое лечение — колоссальная нагрузка на организм: убивая раковые клетки, препараты "убивают" и иммунную систему. Биологи утверждают, что при раковых заболеваниях примерно в половине случаев смерть наступает не из-за собственно разрастающейся опухоли, а из-за вреда, наносимого иммунным клеткам. И по достаточно грубым экспертным оценкам (точных исследований на эту тему пока нет), в четверти-трети случаев этот вред наносят не раковые клетки, а лекарственные препараты. Поэтому сейчас ученые всего мира сосредоточились на иной стратегии в борьбе с раком — "стратегии выживания организма". Они хотят найти терапию, которая позволит перевести острое раковое заболевание в стадию контролируемой хронической ремиссии. "Лечение ракового заболевания — безумно сложная система: раковые клетки размножаются и мутируют, губят нормальные и иммунные клетки, вводимые препараты травят как раковые клетки, так и иммунные, концентрация лекарства в организме постоянно меняется, причем меняется нелинейно. И в рамках этой модели надо придумать такую стратегию лечения, чтобы число раковых клеток было "не смертельно" большим, а число иммунных и нормальных клеток — напротив, "не смертельно" низким. Концентрация лекарственного средства и его суммарное количество — тоже ограниченные величины. В таком фазовом пространстве нужно продержаться как можно дольше, не выходя за его границы. Выйдешь за границу — все, пациент умер", — поясняет профессор Александр Братусь, научный руководитель Егорова и Тодорова. Прежде математики, как правило, не использовали отдельного уравнения для динамики лекарственного средства: они вводили управление непосредственно в уравнения динамики клеток, а функцией цели выбирали интегральные среднеквадратичные функционалы. Однако интегральные среднеквадратичные функционалы по своей природе не могут обеспечить выполнение жестких фазовых ограничений. Это, может, и не смертельно для многих задач механики, но для задач терапии решительно не годится, поскольку выход за фазовое пространство означает гибель пациента. Пять лет назад, в 2009 году, Александр Братусь в своей работе "Синтез оптимального управления в задаче выбора лекарственного воздействия на растущую опухоль" впервые применил метод динамического программирования для решения задач синтеза оптимальной терапии. При этом он описал динамику лекарственного средства отдельным уравнением. Фазовое ограничение на максимальное значение концентрации лекарственного средства выполнялось с помощью введения немонотонной функции терапии, а функционалом задачи было число больных клеток в конечный момент времени. Проект, за который группа Братуся взялась в прошлом году, заключается в разработке методов анализа и алгоритмов поиска стратегии использования лекарственных средств в математических моделях, которые описывают пространственную динамику взаимодействия больных и здоровых клеток с помощью нелинейной системы уравнений в частных производных параболического типа. Важнейшая задача при этом — задача выживания, то есть максимизация времени пребывания системы в безопасных интервалах значений фазовых переменных (число больных, здоровых, иммунных клеток системы и концентрация лекарства). За основу пока что взяли математическую модель одного из самых распространенных видов рака мозга — глиомы. На первом этапе, который стартовал в прошлом году, необходимо было решить задачу определения оптимальных значений интенсивностей и периодов, в течение которых следует применять препарат, а также протяженности режима релаксации.
Бесконечномерная многокритериальная оптимизация


Зависимость концентрации химиотерапевтического агента при α2=0,5
Зависимость концентрации химиотерапевтического агента при α2=0,5


Зависимость концентрации химиотерапевтического агента при α2=0,8
Зависимость концентрации химиотерапевтического агента при α2=0,8


После окончания в 2011 году университета Иван Егоров присоединился к исследованиям профессора Братуся. Как он сам рассказывает, его привлекла сложность и неординарность проблемы: "По сути, из-за того, что лекарство влияет и на больные, и на здоровые клетки, получается задача бесконечномерной многокритериальной оптимизации. А такого практически никогда не было. Даже и постановку-то такой задачи сделать сложно". Кстати, параллельно с учебой в аспирантуре Иван работает в инвестиционном департаменте машиностроительного дивизиона корпорации "Росатом", где тоже занимается многокритериальной оптимизацией, хотя и конечномерной. Он с коллегами разработал методику и программный комплекс для построения системы градации иерархии инвестпроектов по степени их важности и востребованности. Для построения оптимальной стратегии терапии рака решено было воспользоваться моделью российского физика Натальи Степановой — пионера в области фотодинамической терапии рака. Работая на физфаке и мехмате МГУ, Наталья Степанова разработала и в 1980 году представила одну из первых в мире модель роста злокачественных опухолей, учитывающую реакцию иммунной системы. До нее при решении задач оптимального управления в биологии принимались во внимание только размер опухоли и количество лекарственного препарата, учет иммунной реакции в уравнение не добавлялся. Биологи МГУ, с которыми Егоров обсуждал эту проблему, считают, что именно модель Степановой наиболее корректна с медицинской точки зрения: если в других моделях предполагается, что лекарство сразу влияет на клетки, то у Степановой принимается во внимание то обстоятельство, что лекарство сначала накапливается в организме и только потом начинает действовать. Иван Егоров выделяет три основные сложности задачи, которой он занимается. Во-первых, это нелинейные системы, которые, в отличие от линейных, математикой пока изучены слабовато и у которых на порядок больше различных особенностей, чем у линейных систем. Во-вторых, системы, с которыми приходится работать, — многомерные, как минимум 3 - 4-мерные. Конечно же, существуют численные методы для решения задач, в том числе оптимального управления и динамического программирования. Но здесь у нас возникают сложности третьего типа: а) если какая-то задача решается численно, то для нее нужно выделять ограниченную область пространства. Но это отдельный большой и серьезный вопрос — как ее корректно определить: нужно исследовать асимптотику, проводить дополнительный анализ; б) если и находится какой-то численный метод решения задачи, то теоремы сходимости этого численного метода либо отсутствуют, либо содержат такие предположения, которые невозможно проверить, или же они не выполняются. "Вообще, такая загвоздка — обычное явление в математике, даже в задачах конечномерной оптимизации, — сетует Егоров. — Начинаешь искать локальный экстремум самым простейшим методом градиентного спуска, исследуешь функцию, а градиента-то у нее и нет"; в) численные методы не дают качественной картины. Поэтому Егоров и Тодоров разработали не сугубо вычислительные, а численно-аналитические методы, которые содержат аналитическую составляющую и позволяют выявить качественную структуру решения. Пока что исследование проводится только для монотонно возрастающих функций терапии, которые не учитывают пороговый эффект: когда лекарства слишком много, его эффективность снижается. Модифицированная модель Степановой (динамика роста злокачественной опухоли с соответствующей реакцией иммунной системы при воздействии химиотерапевтического агента) выглядит тогда как система уравнений:
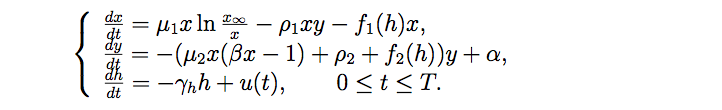
где x — объем опухоли, y — плотность иммунокомпетентных клеток, h — концентрация химиотерапевтического агента; x∞ - вместимость (потенциальная емкость) опухоли, µ1 и α определяют скорости роста численностей опухолевых и иммунокомпетентных клеток соответственно, ρ1 и ρ2 — показатели их смертности, выражение µ2x (βx – 1) y с положительными параметрами µ2, β описывает взаимодействие между двумя типами клеток, т. е. зависимость иммунной реакции от численности опухолевых клеток.
Негативное влияние химиотерапевтического агента на опухолевые и иммунокомпетентные клетки задается функциями терапии f1 (h), f2 (h). В последнем дифференциальном уравнении ϒh можно интерпретировать как параметр диссипации (распространения) химиотерапевтического агента, а u (·) ∈ L∞ ( [0, T], R) — управляющая функция, представляющая поступление препарата в организм пациента. Допустимые управления удовлетворяют ограничению 0≤u (t)≤R∀t [0, T] с фиксированной положительной константой R. Задача, таким образом, состоит в отыскании оптимального управления в форме обратной связи, доставляющего минимум функционалу:
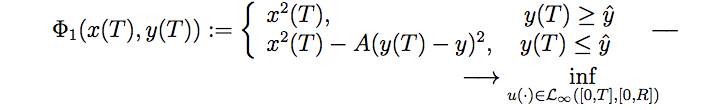
Здесь T > 0 — фиксированный конечный момент времени, параметр y? характеризует приемлемый уровень иммунной реакции, A — достаточно большая положительная константа, так называемый штрафной коэффициент, который отвечает за малые значения иммунной реакции в конечный момент времени (чтобы иммунная система не погибла).
Система исследуется принципом максимума Понтрягина, и алгоритм синтеза оптимального управления получается двухэтапным: на первом этапе (интенсивная терапия) поступление препарата в организм пациента максимально, затем в определенной точке фазового пространства (которая найдена аналитически и характеризуется фазовыми координатами и временем) стадия активной терапии прерывается и сменяется этапом релаксации. При этом чем сильнее препарат влияет на иммунную систему, тем короче стадия активной терапии и соответственно продолжительней режим релаксации (рис. 01, 02).
Дмитрий Романовский
Русский врач, считается основоположником химиотерапии. Он установил, что хинин повреждает малярийных плазмодиев.

Пауль Эрлих
Немецкий врач, лауреат Нобелевской премии за 1908 год. Предложил термин "химиотерапия", он же обнаружил, что микробы могут приобретать устойчивость к химическим препаратам, и стал применять химиотерапию при злокачественных заболеваниях.

На очереди — математическая модель ангиогенеза
Таким образом, найдено оптимальное отношение времени активной терапии к времени релаксации, а также оптимальное значение интенсивности применяемого лекарственного средства. Теперь группа профессора Братуся работает над введением в систему фактора, который учитывает возникновение в процессе терапии раковых клеток, устойчивых к препарату ("резистентные" клетки). Поскольку динамика процесса превращения обыкновенных раковых клеток в резистентные, а также перехода этих клеток снова в первоначальное состояние еще не до конца изучена, приходится рассматривать модель, в которой с некоторой вероятностью каждая из обыкновенных и резистентных раковых клеток делится снова на обыкновенную раковую клетку и резистентную.
Следующим этапом работы над проектом будет добавление в систему уравнения, описывающего поток питательных веществ через кровеносные сосуды (кислород, глюкоза). Раковые клетки более устойчивы к нехватке кислорода, чем здоровые. Это приводит к росту расхода питательных веществ, кислородному голоданию и гибели здоровых клеток. Выполнение этой части проекта позволит создать предпосылки для математической модели исключительно важного явления — ангиогенеза, которое характеризуется выработкой новых питательных ресурсов (сосудов), предназначенных для питания все возрастающего числа раковых клеток.
В статье использованы материалы работы "On Viable Therapy Strategy for a Mathematical Spatial Cancer Model Describing the Dynamics of the Malignant and Healthy Cells" (авторы — Александр Братусь, МГУ им. М. В. Ломоносова, Россия; Светлана Коваленко, Федеральный научно-клинический центр Федерального медико-биологического агентства, Россия; Еле на Фиммель, Университет прикладных наук Мангейма, Германия)

